Zubair Khalid
Department of Electrical Engineering
Syed Babar Ali School of Science and Engineering
Lahore University of Management Sciences.
Novel Spherical Harmonic Transform (NSHT) - MATLAB Toolbox
Introduction
NSHT Toolbox is a MATLAB based toolbox for spherical harmonic analysis on the sphere. It implements the novel spherical harmonic transform (NSHT) of a band-limited signal using the optimal number of samples.
Overview
For the accurate representation of a signal on the sphere band-limited at degree 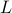 with
with 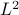 degrees of freedom in the spectral domain, we developed a new sampling scheme in [1] that requires
degrees of freedom in the spectral domain, we developed a new sampling scheme in [1] that requires 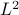 on the sphere. Thus, the sampling scheme matches the spectral dimensionality of the signal.
on the sphere. Thus, the sampling scheme matches the spectral dimensionality of the signal.
For the sampling scheme, we also developed spherical harmonic transform, referred as novel spherical harmonic transform, which is implemented in this toolbox. The spherical harmonic transforms (forward and inverse) allow the computation of transforms with sufficient accuracy and manageable computational complexity and do not require any pre-computation associated with spherical harmonic transforms. The pre-computation is only required to determine the optimal placement of samples on the sphere. Once optimal sample positions are determined, the implementation of SHT does not require any pre-computation.
If you use NSHT toolbox for harmonic analysis which results in publication, please reference the site (http:www.zubairkhalid.org/nsht) and our related academic paper:
[1] Z. Khalid, R. A. Kennedy and J. D. McEwen, “An Optimal-Dimensionality Sampling Scheme on the Sphere for Fast Spherical Harmonic Transforms,” IEEE Trans. Signal Process., vol. 62, no. 17, pp. 4597-4610, September 2014. (IEEE Xplore) (arXiv)
Authors and Affiliations
Zubair Khalid
Research School of Engineering, The Australian National UniversityRodney A. Kennedy
Research School of Engineering, The Australian National UniversityJason D. McEwen
Mullard Space Science Laboratory, University College London
Download
The source code of the NSHT toolbox can be downloaded from here (version: 0.9b).
We provide this code in the hope that it will be useful, but WITHOUT ANY WARRANTY.
If you notice an error or bug or need support, please write to zubair.khalid@anu.edu.au.
Version History
Current version: 0.9b (15 Aug. 2014), Public release of first beta.
License
NSHT toolbox to compute spherical harmonic transforms and carry out harmonic analysis Copyright (C) 2014 Zubair Khalid
This program is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version.
This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.
You should have received a copy of the GNU General Public License along with this program. If not, see http:www.gnu.org/licenses.
Installation Instructions
Once you download the toolbox as nsht.zip, unzip the code to the directory ‘nsht’.
The MATLAB working directory or path should be set for directory ‘nsht’ which contains the ‘src’ directory, file ‘nsht_install.m’ and nsht demos.
For working directory: nsht, execute the file ‘nsht_install.m’. The installation creates a mex function for the computation of associated Legendre polynomials, which significantly improves the computation time. The installation also checks that the pre-computed optimal sample positions are available in the src/Data directory.
Notes: The band-limit supported in the current version (0.9b) is 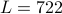 . The NSHT is shown to compute sufficiently accurate spherical harmonic transform up to band-limit
. The NSHT is shown to compute sufficiently accurate spherical harmonic transform up to band-limit 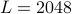 . However, the optimal sample positions have been pre-computed up to
. However, the optimal sample positions have been pre-computed up to 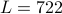 .
.
Installation Requirements: MATLAB with the support of codegen and mex compiler.
Notes on Installation Requirements: For efficient implementation of spherical harmonic transforms, the associated Legendre functions are computed in C. This computation is implemented using MATLAB codegen that generates a C code and mex function from MATLAB code. The mex function is then used for computation. If MATLAB is not supported by mex compiler, the toolbox can still be used. However, it takes more computation time to compute spherical harmonic transform.
Documentation
There is documentation for the MATLAB functions within the source files, which can be accessed through the help or doc command in MATLAB.
Functions
List of MATLAB functions with brief description is provided here.
The documentation for each function in MATLAB can be obtained using the command: doc <function name>.
nsht_forward
Computes forward spherical harmonic transform.
nsht_indexed_theta
Determine sample positions along co-latutude.
nsht_inverse
Computes inverse spherical harmonic transform.
nsht_legmat
Compute Legendre matrix.
nsht_ordered_theta
Determine the optimal placement of rings along theta.
nsht_plot_sampling
Plots the sampling points on the sphere over the surface of the sphere.
nsht_plot_spectral
Plots the spectral representation of the signal as a surface plot for different degrees and orders.
nsht_plot_sphere
Plots the function on the sphere over the sample points in the proposed sampling scheme.
nsht_sampling_points
Determine the sampling points on the sphere for the sampling scheme proposed in the following paper.
nsht_sharmonic
Compute spherical harmonic over optimal sampling spatial grid.
nsht_sharmonic_g
Compute spherical harmonic over given spatial grid.
nsht_sharmonic_matrix
Computes spherical harmonic of all degrees and orders less than  over given spatial grid.
over given spatial grid.
Demos (Examples)
nsht_demo1
Plots sampling points on the sphere required for accurate computation of spherical harmonic band-limited signal
nsht_demo2
Record the computation times to carry out forward and inverse spherical harmonic transform (SHT) using random data.
nsht_demo3
Record the computation times to carry out forward and inverse spherical harmonic transform (SHT) using Earth topographic data.
nsht_demo4
Generate spherical harmonic  of degree
of degree 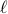 and order
and order 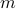 over the grid defined by band-limit
over the grid defined by band-limit 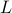 .
.
Accuracy Analysis
We randomly generate the complex valued band-limited test signal 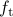 with real and imaginary parts uniformly distributed in the interval
with real and imaginary parts uniformly distributed in the interval ![[-1,,1]](eqs/377526509-130.png) over the
over the 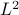 samples of our sampling scheme. The forward SHT, followed by inverse SHT is applied on the test signal to obtain the reconstructed signal
samples of our sampling scheme. The forward SHT, followed by inverse SHT is applied on the test signal to obtain the reconstructed signal 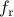 band-limited at
band-limited at 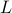 .
.
We repeat the experiment 10 times and then obtain the average values for the maximum reconstruction error  and the mean reconstruction error
and the mean reconstruction error 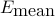 between the test signal
between the test signal 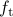 and reconstructed signal
and reconstructed signal 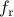 . See our paper [1] for
details.
. See our paper [1] for
details.
Both  and
and  are plotted below for the band-limit in the range
are plotted below for the band-limit in the range 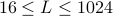 .
.
 |
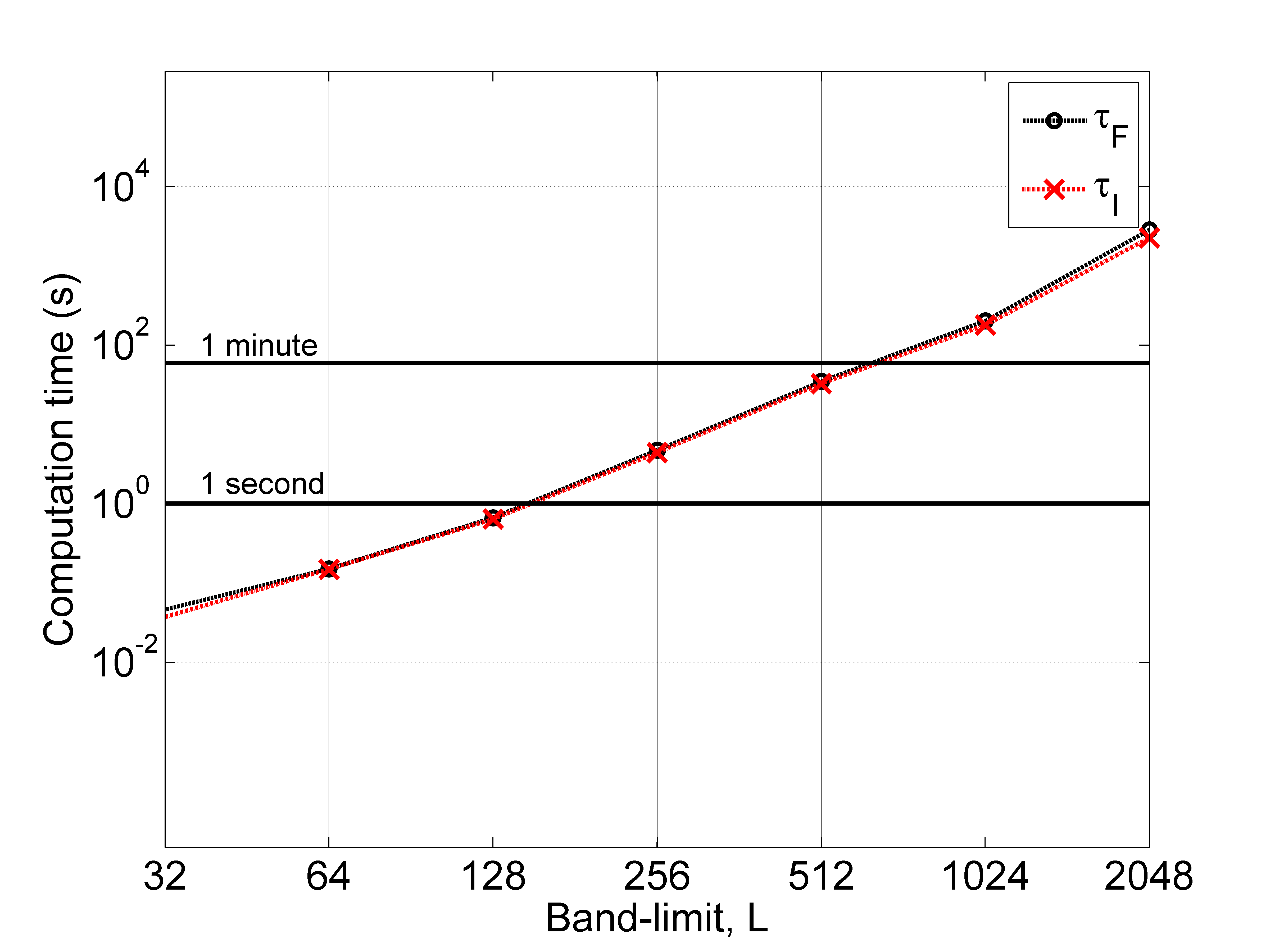
Computation Times
We measure the computation times, denoted by 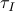 and
and 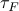 to carry out the proposed inverse and forward transforms, respectively.
to carry out the proposed inverse and forward transforms, respectively.
The computation times are recorded using NSHT MATLAB Toolbox running on a machine equipped with 2.6 GHz Intel Core i7 processor and 64 GB of RAM.
The computation times 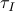 and
and 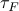 in seconds, averaged over 10 different signals, are plotted below.
in seconds, averaged over 10 different signals, are plotted below.
 |